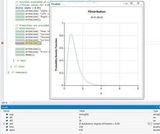
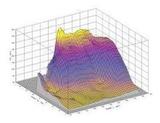
Análisis de Datos
Autoría y LMS
Colaboración Y Diseño
Desarrolo low code, soluciones e integraciones vía APIs
DevSecOps
Gestión de Proyectos e ITSM
Infraestructura y Ciberseguridad
Ingeniería & Gis

Licenciamiento de Software y contrato paraguas